实验题目
为之前的五级流水线 CPU 设计 cache 模块,体会 cache 对内存读写性能的影响。
实验目的
在计算机系统中,CPU 高速缓存是用于减少处理器访问内存所需平均时间的部件。在金字塔式存储体系中它位于自顶向下的第二层,仅次于 CPU 寄存器。其容量远小于内存,但速度却可以接近处理器的频率。
当处理器发出内存访问请求时,会先查看缓存内是否有请求数据。如果存在(命中),则不经访问内存直接返回该数据;如果不存在(失效),则要先把内存中的相应数据载入缓存,再将其返回处理器。
缓存之所以有效,主要是因为程序运行时对内存的访问呈现局部性(Locality)特征。这种局部性既包括空间局部性(Spatial Locality),也包括时间局部性(Temporal Locality)。有效利用这种局部性,缓存可以达到极高的命中率。
实验内容
在本次实验,我们假设现在内存大小 $1024 \times 16bit$,需要设计 $256 \times 16bit$ 大小的 data memory cache,使用二路组相联,使用 LRU 置换策略。
缓存的存储结构
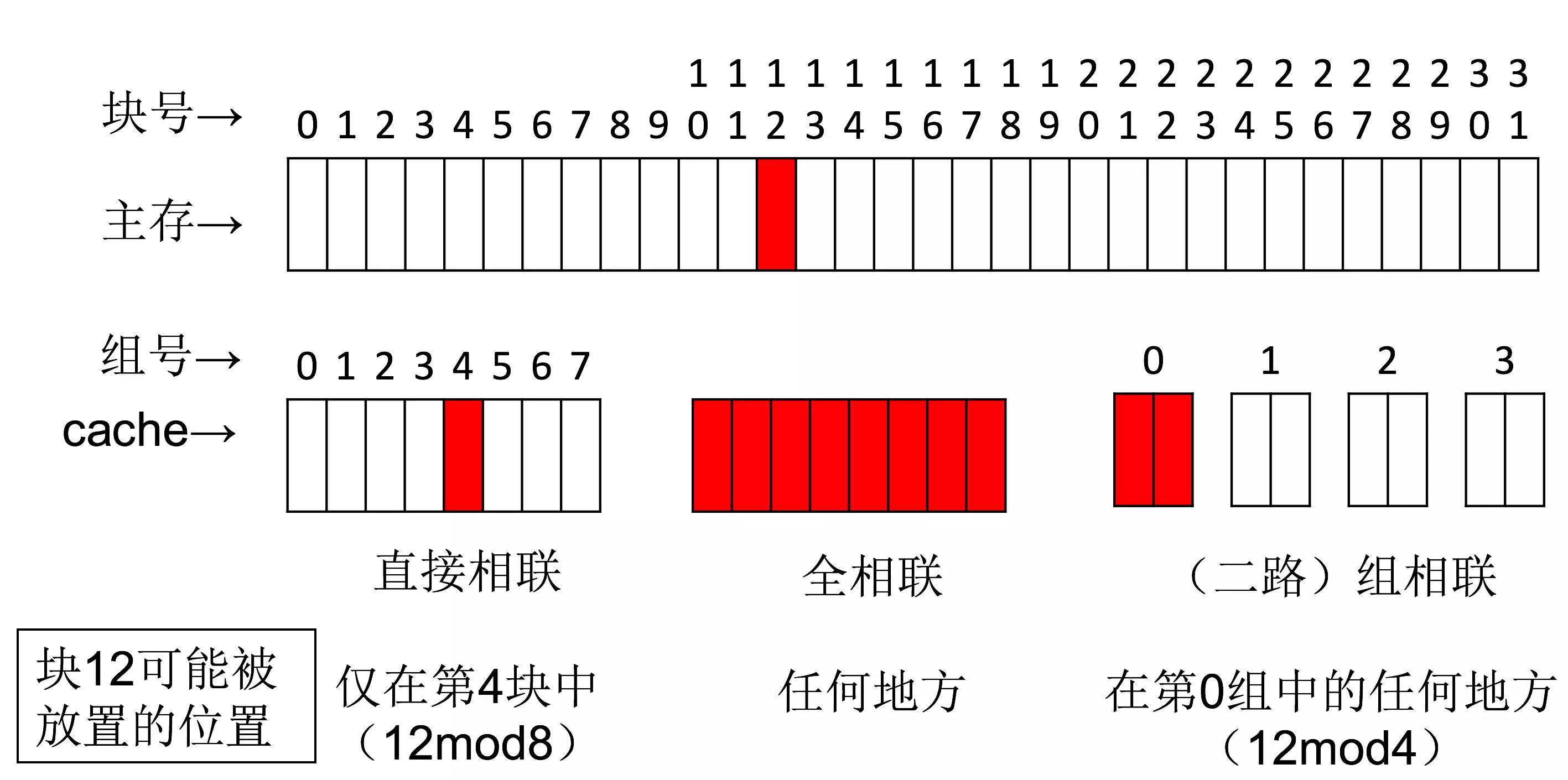
直接映射
为了便于数据查找,一般规定内存数据只能置于缓存的特定区域。对于直接映射缓存,每一个内存块地址都可通过模运算对应到一个唯一缓存块上。注意这是一种多对一映射:多个内存块地址须共享一个缓存区域。
$I = A_{mb}\mod N$
其中I为缓存索引,Amb为内存块地址,N为缓存块总数。
使用内存块地址而不是内存地址是因为缓存块通常包含一组连续的内存单元数据。以缓存块为32字节的直接映射缓存为例,内存地址Am到缓存索引的计算为
$I = \left( A_m\div 32 \right) \mod N$
由于缓存字节数和缓存块数均为 2 的幂,上述运算可以由硬件通过移位极快地完成。
N 路组相联
直接匹配缓存尽管在电路逻辑上十分简单,但是存在显著的冲突问题。由于多个不同的内存块仅共享一个缓存块,一旦发生缓存失效就必须将缓存块的当前内容清除出去。这种做法不但因为频繁的更换缓存内容造成了大量延迟,而且未能有效利用程序运行期所具有的时间局部性。
组相联(Set Associativity)是解决这一问题的主要办法。使用组相联的缓存把存储空间组织成多个组,每个组有若干数据块。通过建立内存数据和组索引的对应关系,一个内存块可以被载入到对应组内的任一数据块上。
$I = \left( A_m\div Nw\div N_a \right) \mod N$
其中,I 为缓存索引,Am 为内存地址,Nw 为缓存块内字数, Na 为相联路数, N 为组数。当使用组相联时,在通过索引定位到对应组之后,必须进一步地与所有缓存块的标签值进行匹配,以确定查找是否命中。这在一定程度上增加了电路复杂性,因此会导致查找速度有所降低。
直接匹配可以被认为是单路组相联。
全相联
组相联的一个极端是全相联。这种缓存意味着内存中的数据块可以被放置到缓存的任意区域。这种相联完全免去了索引的使用,而直接通过在整个缓存空间上匹配标签进行查找。由于这样的查找造成的电路延迟最长,因此仅在特殊场合,才会使用。
置换策略
对于组相联缓存,当一个组的全部缓存块都被占满后,如果再次发生缓存失效,就必须选择一个缓存块来替换掉。存在多种策略决定哪个块被替换。
显然,最理想的替换块应当是距下一次被访问最晚的那个。这种理想策略无法真正实现,但它为设计其他策略提供了方向。
FIFO
替换掉进入组内时间最长的缓存块。
LRU
跟踪各个缓存块的使用状况,并根据统计比较出哪个块已经最长时间未被访问。但对于 2 路以上相联,这个算法的时间代价会非常高。
随机替换法
顾名思义,随机替换掉一个块,但有的测试表明完全随机替换的性能近似于LRU。
NMRU
近似是非最近使用算法,这个算法仅记录哪一个缓存块是最近被使用的。在替换时,会随机替换掉任何一个其他的块。故称非最近使用。相比于LRU,这种算法仅需硬件为每一个缓存块增加一个使用位(use bit)即可。
回写策略
为了和下级存储(如内存)保持数据一致性,就必须把数据更新适时传播下去。这种传播通过回写来完成。一般有两种回写策略:写回(Write back)和写通(Write through)。
写回(Write back)
写回是指,仅当一个缓存块需要被替换回内存时,才将其内容写入内存。如果缓存命中,则总是不用更新内存。为了减少内存写操作,缓存块通常还设有一个脏位(dirty bit),用以标识该块在被载入之后是否发生过更新。如果一个缓存块在被置换回内存之前从未被写入过,则可以免去回写操作。
写回的优点是节省了大量的写操作。这主要是因为,对一个数据块内不同单元的更新仅需一次写操作即可完成。
写通(Write through)
写通是指,每当缓存接收到写数据指令,都直接将数据写回到内存。如果此数据地址也在缓存中,则必须同时更新缓存,这种设计会引发造成大量写内存操作。
写通较写回易于实现,并且能更简单地维持数据一致性。
架构设计
根据缓存的大小,我们把内存划分为下面的三段,但在本次 cache 设计中用不到 offset。
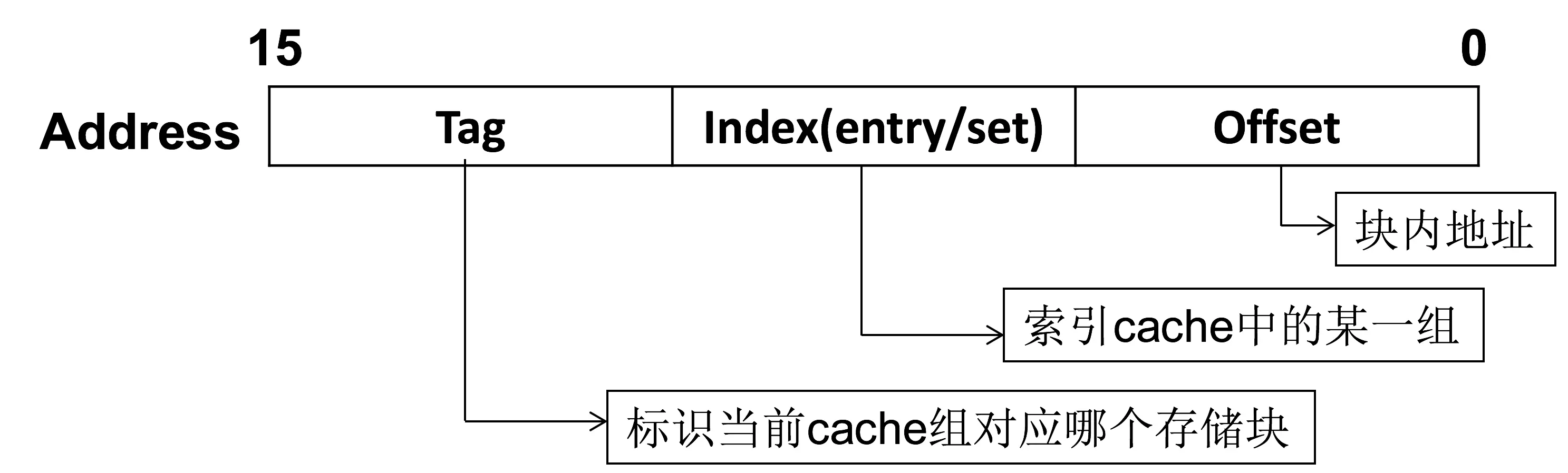
- Index 对应缓存块的块号,即在十进制中取模后的部分。在本次实验中,块号为 0-127,即是内存地址的低七位。
- 由于这是一种多对一映射,必须在存储一段数据的同时标示出这些数据在内存中的确切位置。所以每个缓存块都配有一个标签(Tag)。
拼接标签值和此缓存块的索引,即可求得缓存块的内存地址,如果再加上块内偏移,就能得出任意一块数据的对应内存地址。此外,每个缓存块还对应若干标志位,包括有效位(valid bit)、脏位(dirty bit)、使用位(use bit)等。

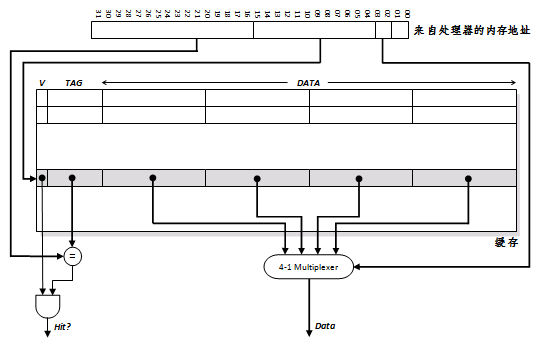
例图为 32bit CPU 直接映射的 cache 设计
运作流程
下面简要描述本次设计的 cache 的工作流程。这个双路组相联缓存共有 256 个缓存块,每路 128 个,置换策略为 LRU,使用写通(Write through)策略维持数据一致性。
LOAD 指令
- 用索引定位到相应的缓存块。
- 用标签尝试匹配两路缓存块的对应标签值,如果存在这样的匹配且使用位(use bit)为 True,称为命中(Hit),否则称为未命中(Miss)。
- 如命中,将数据取出,送回处理器,并且将本路缓存块计数器(counter)置 0,另外一路 +1。
- 如未命中,从内存取出对应位置的数据,如果有使用位(use bit)为 False 的缓存块,使用之,否则替换掉计数器(counter)比较大的一路的缓存块,最后使用位(use bit)置 True,计数器(counter)置 0。
STORE 指令
- 用索引定位到相应的缓存块。
- 用标签尝试匹配该缓存块的对应标签值。其结果为命中或未命中。
- 如命中,同时将数据写入缓存块和内存,并且将本路缓存块计数器(counter)置 0,另外一路 +1。
- 如未命中,将数据写入内存,如果有使用位(use bit)为 False 的缓存块,写入之,否则替换掉计数器(counter)比较大的一路的缓存块,最后使用位(use bit)置 True,计数器(counter)置 0。
特别说明
本次设计的 cache 与现实计算机的 cache 组成架构并不相同。实际计算机中,CPU 的运行速度比内存块得多,例如下图,可以看到 CPU 的频率为 2.7 GHz,而且还是双核心,而内存只有 1867 MHz。一般来说,读取内存时候,CPU 需要处于 stall 状态,被阻塞。

而在这个简单的五级流水线 CPU 最开始设计的时候,Jun Wang 就没有考虑到后来要添加 cache 的情况,所以内存的频率就比 CPU 频率高,导致内存对于 CPU 来说是可随时读写的,所以实际上这个架构设计 cache 是没有存在的必要的。但是我们仍可以设计 cache,最后统计 hit rate 和 miss rate 来计算 cache 节省的时间和衡量不同替换算法的性能。当然其实写高级语言模拟一个出来更加方便,但是……
至于为何不改为内存比 CPU 慢的架构,那是因为期末太忙了……
代码等过了 DDL 再放吧,不然会出事的...
已决定弃坑,期末太忙……
晚上睡不着,把 Bug 修完了,一个没什么意义的 cache。
代码设计
我将 cache 设计成内存读写的 interface,这样只需要在 MEM 模块将读内存改为读 cache,然后一切处理在 CACHE 模块完成。
在仿真的时候遇到一个问题就是 for 循环初始化数组会导致 ISim 失去响应,问了滔神说 for 循环有坑,所以机智的我掏出了 Python。
#!/usr/bin/python
for i in range(1, 128):
print 'cache0[%d] <= 0;\ncache1[%d] <= 0;'%(i,i)
此外,我在统计 rate 的时候耍了个 little trick。因为我设定的 cache 的时序比 CPU 刚好高一倍,所以如果 CPU 读写 miss 一次,对于 cache 就是 miss 一次,hit 一次,所以统计的时候需要注意。
最后附上使用双路组相联缓存,共有 256 个缓存块,LRU 算法对 1024 个数进行冒泡排序的结果。

hit count = 2454266,miss count = 476160,hit rate = 83.75%。
至于不同算法,size 之间的对比分析,还有是修正时序的版本,有时间再继续跳坑吧……
最后丢下代码,View Code on GitHub: bazingaterry/Mipu。
Reference: zh.wikipedia.org/wiki/CPU缓存